- 重要な情報
- はじめに
- Datadog
- Datadog サイト
- DevSecOps
- AWS Lambda のサーバーレス
- エージェント
- インテグレーション
- コンテナ
- ダッシュボード
- アラート設定
- ログ管理
- トレーシング
- プロファイラー
- タグ
- API
- Service Catalog
- Session Replay
- Continuous Testing
- Synthetic モニタリング
- Incident Management
- Database Monitoring
- Cloud Security Management
- Cloud SIEM
- Application Security Management
- Workflow Automation
- CI Visibility
- Test Visibility
- Intelligent Test Runner
- Code Analysis
- Learning Center
- Support
- 用語集
- Standard Attributes
- ガイド
- インテグレーション
- エージェント
- OpenTelemetry
- 開発者
- 認可
- DogStatsD
- カスタムチェック
- インテグレーション
- Create an Agent-based Integration
- Create an API Integration
- Create a Log Pipeline
- Integration Assets Reference
- Build a Marketplace Offering
- Create a Tile
- Create an Integration Dashboard
- Create a Recommended Monitor
- Create a Cloud SIEM Detection Rule
- OAuth for Integrations
- Install Agent Integration Developer Tool
- サービスのチェック
- IDE インテグレーション
- コミュニティ
- ガイド
- API
- モバイルアプリケーション
- CoScreen
- Cloudcraft
- アプリ内
- Service Management
- インフラストラクチャー
- アプリケーションパフォーマンス
- APM
- Continuous Profiler
- データベース モニタリング
- Data Streams Monitoring
- Data Jobs Monitoring
- Digital Experience
- Software Delivery
- CI Visibility (CI/CDの可視化)
- CD Visibility
- Test Visibility
- Intelligent Test Runner
- Code Analysis
- Quality Gates
- DORA Metrics
- セキュリティ
- セキュリティの概要
- Cloud SIEM
- クラウド セキュリティ マネジメント
- Application Security Management
- AI Observability
- ログ管理
- Observability Pipelines(観測データの制御)
- ログ管理
- 管理
回帰
ロバスト回帰
| 関数 | 説明 | 例 |
|---|---|---|
robust_trend() | Huber 損失を使用して、ロバスト回帰傾向線を求めます。 | robust_trend(avg:<METRIC_NAME>{*}) |
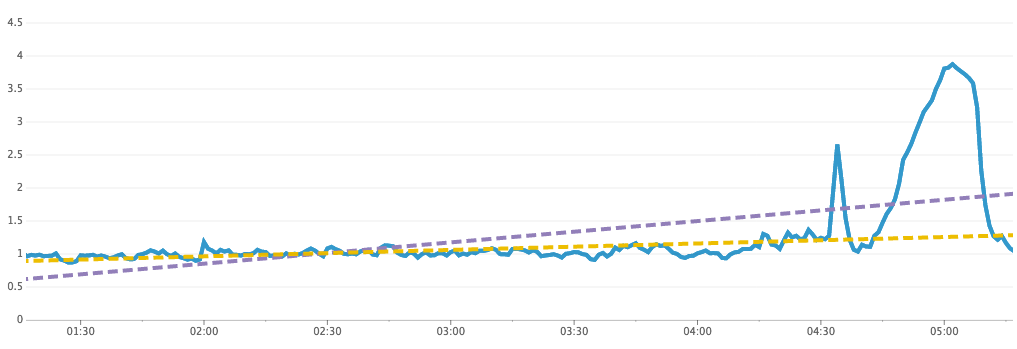
最も一般的な線形回帰である最小二乗法 (OLS) は、極値ポイントが少数あるだけでも大きな影響を受けがちです。ロバスト回帰も回帰直線を求める方法の 1 つですが、少数の極値からはそれほど強い影響を受けません。例として、次のプロットを見てみます。
元のメトリクスは青い実線で示されています。紫の破線は OLS 回帰線で、黄色の破線がロバスト回帰線です。メトリクスにある短時間のスパイクによって OLS 回帰線はやや上向きになりますが、ロバスト回帰線はこのスパイクを無視し、メトリクスの全体的傾向により的確に沿っています。
傾向線
| 関数 | 説明 | 例 |
|---|---|---|
trend_line() | メトリクス値に沿う最小二乗法の回帰線を求めます。 | trend_line(avg:<METRIC_NAME>{*}) |
例:
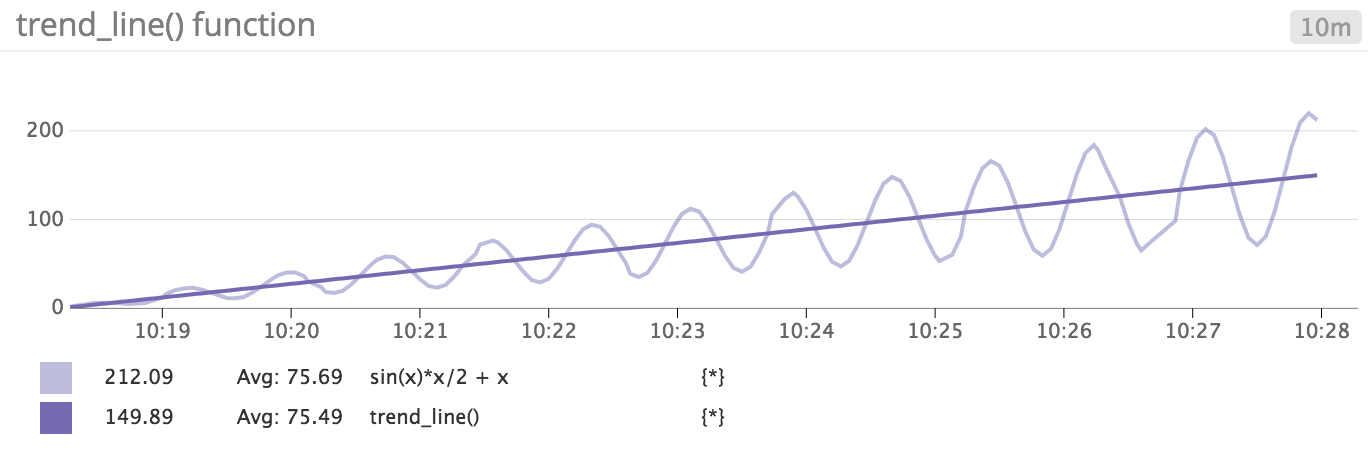
関数 sin(x) * x/2 + x、trend_line(sin(x) * x/2 + x) は、次のようになります。
区分的定数
| 関数 | 説明 | 例 |
|---|---|---|
piecewise_constant() | 複数の定数値区間で構成される区分的関数でメトリクスを近似します。 | piecewise_constant(avg:<METRIC_NAME>{*}) |
例:
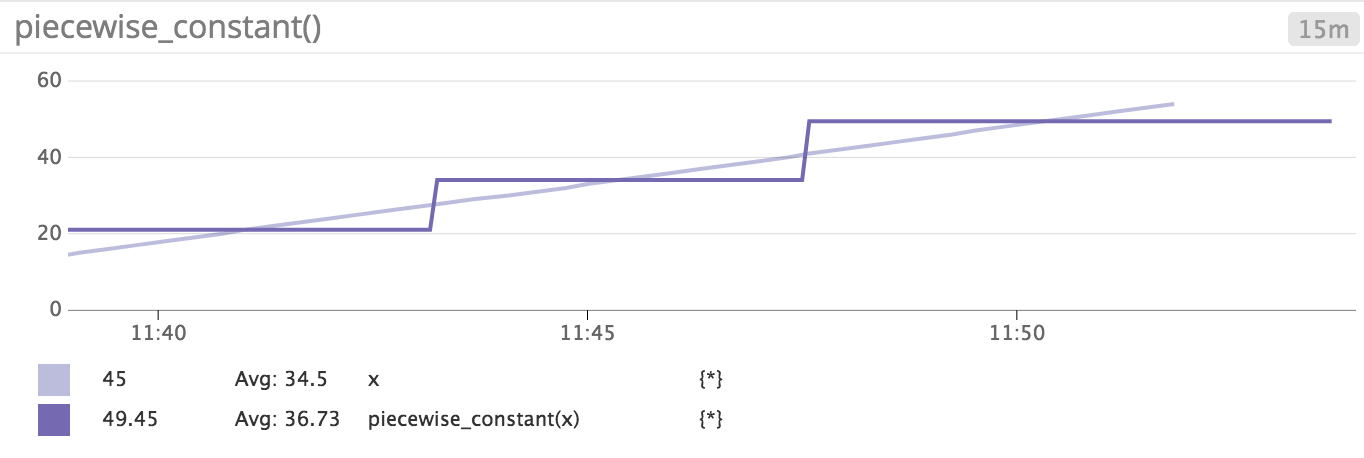
関数 x、piecewise_constant(x) は、次のようになります。
その他の関数
他に利用できる関数を参照します。
- アルゴリズム: メトリクスに異常値や外れ値の検出機能を実装します。