- Principales informations
- Getting Started
- Datadog
- Site Datadog
- DevSecOps
- Serverless for AWS Lambda
- Agent
- Intégrations
- Conteneurs
- Dashboards
- Monitors
- Logs
- Tracing
- Profileur
- Tags
- API
- Service Catalog
- Session Replay
- Continuous Testing
- Surveillance Synthetic
- Incident Management
- Database Monitoring
- Cloud Security Management
- Cloud SIEM
- Application Security Management
- Workflow Automation
- CI Visibility
- Test Visibility
- Intelligent Test Runner
- Code Analysis
- Learning Center
- Support
- Glossary
- Standard Attributes
- Guides
- Agent
- Intégrations
- OpenTelemetry
- Développeurs
- Authorization
- DogStatsD
- Checks custom
- Intégrations
- Create an Agent-based Integration
- Create an API Integration
- Create a Log Pipeline
- Integration Assets Reference
- Build a Marketplace Offering
- Create a Tile
- Create an Integration Dashboard
- Create a Recommended Monitor
- Create a Cloud SIEM Detection Rule
- OAuth for Integrations
- Install Agent Integration Developer Tool
- Checks de service
- IDE Plugins
- Communauté
- Guides
- API
- Application mobile
- CoScreen
- Cloudcraft
- In The App
- Dashboards
- Notebooks
- DDSQL Editor
- Alertes
- Infrastructure
- Métriques
- Watchdog
- Bits AI
- Service Catalog
- API Catalog
- Error Tracking
- Service Management
- Infrastructure
- Universal Service Monitoring
- Conteneurs
- Sans serveur
- Surveillance réseau
- Cloud Cost
- Application Performance
- APM
- Profileur en continu
- Database Monitoring
- Agent Integration Overhead
- Setup Architectures
- Configuration de Postgres
- Configuration de MySQL
- Configuration de SQL Server
- Setting Up Oracle
- Setting Up MongoDB
- Connecting DBM and Traces
- Données collectées
- Exploring Database Hosts
- Explorer les métriques de requête
- Explorer des échantillons de requêtes
- Dépannage
- Guides
- Data Streams Monitoring
- Data Jobs Monitoring
- Digital Experience
- RUM et Session Replay
- Product Analytics
- Surveillance Synthetic
- Continuous Testing
- Software Delivery
- CI Visibility
- CD Visibility
- Test Visibility
- Exécuteur de tests intelligent
- Code Analysis
- Quality Gates
- DORA Metrics
- Securité
- Security Overview
- Cloud SIEM
- Cloud Security Management
- Application Security Management
- AI Observability
- Log Management
- Pipelines d'observabilité
- Log Management
- Administration
Régression
Évolution tendancielle robuste
| Fonction | Description | Exemple |
|---|---|---|
robust_trend() | Ajuste une ligne de tendance de régression robuste grâce à la fonction de perte de Huber. | robust_trend(avg:<NOM_MÉTRIQUE>{*}) |
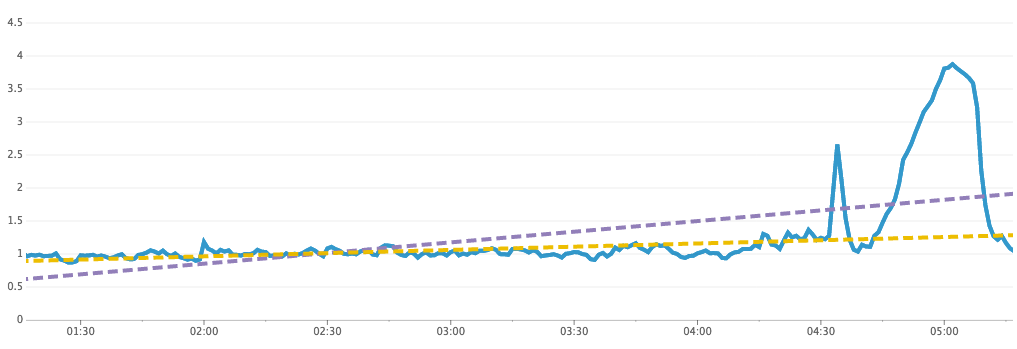
La méthode des moindres carrés ordinaire (MCO) est le type le plus courant de régression linéaire. Elle peut être grandement influencée par un petit nombre de points avec des valeurs extrêmes. La régression robuste est une méthode alternative qui n’est pas autant influencée par un petit nombre de valeurs extrêmes. Prenons comme exemple le graphique suivant.
La métrique d’origine est représentée par une ligne bleue continue. La ligne violette en pointillés est une ligne de régression MCO et la ligne jaune en pointillés est une ligne de régression robuste. Le seul pic de courte durée de la métrique engendre une ligne de régression MCO qui suit une tendance à la hausse, mais la ligne de régression robuste ignore ce pic et reflète davantage la tendance générale de la métrique.
Ligne de tendance
| Fonction | Description | Exemple |
|---|---|---|
trend_line() | Ajuste une ligne de régression des moindres carrés ordinaire en fonction des valeurs des métriques. | trend_line(avg:<NOM_MÉTRIQUE>{*}) |
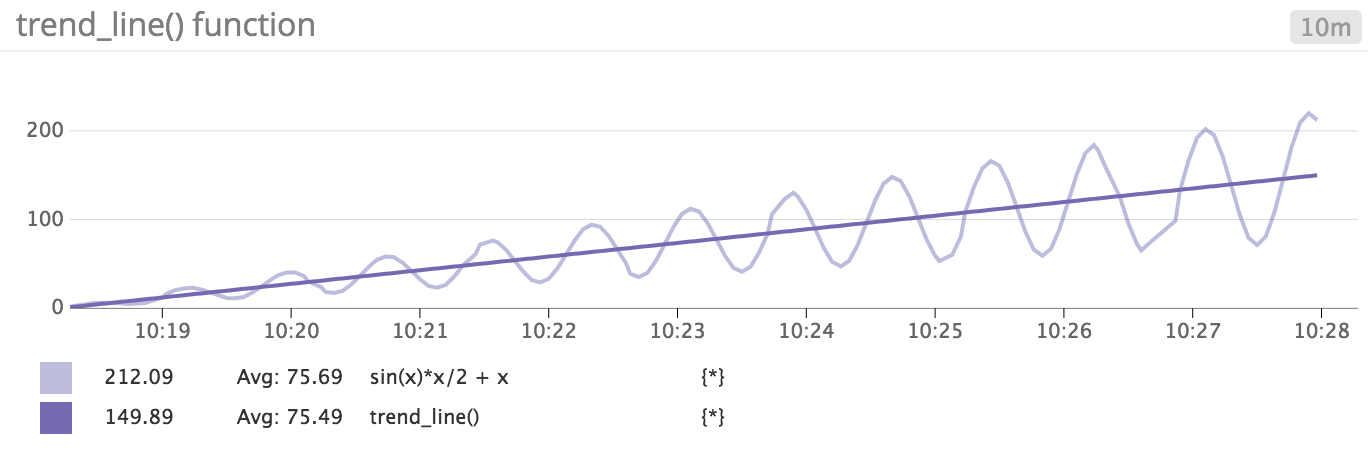
Exemple :
Pour la fonction sin(x) * x/2 + x, trend_line(sin(x) * x/2 + x) donne le graphique suivant :
Fonction constante par morceaux
| Fonction | Description | Exemple |
|---|---|---|
piecewise_constant() | Réalise une estimation de la métrique à l’aide d’une fonction par morceaux composée de segments avec des valeurs constantes. | piecewise_constant(avg:<NOM_MÉTRIQUE>{*}) |
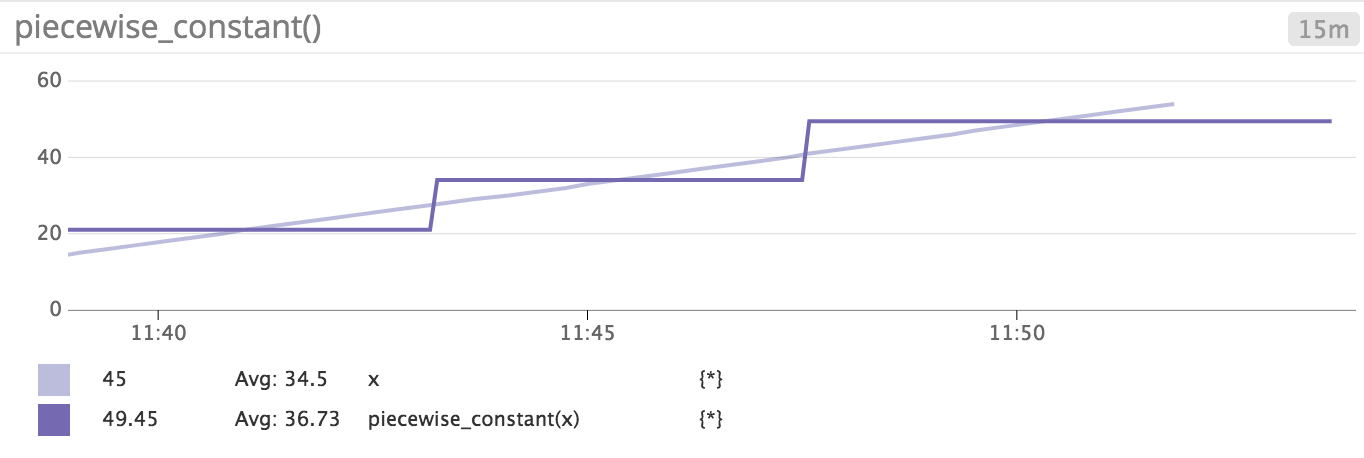
Exemple :
Pour la fonction x, piecewise_constant(x) donne le graphique suivant :
Autres fonctions
Consultez les autres fonctions disponibles :
- Algorithme : mettez en place un système de détection d'anomalies ou de singularités.